Hier finden Sie Information über:
Geländeaufnahme
Streckenberechnung in der Projektion
Streckenberechnung in der Abwicklung
Flächenberechnung in der Projektion
mit dem lustigen Bastelbogen für's Gauss-Elling-Rechnen
wie man mit einer Excel-Tabelle Gauss-Elling rechnet
Flächenberechnung in der Abwicklung
wie man mit einer Excel-Tabelle die Heronscher Formel rechnet
Dreiecksvermaschung nach GAEB-VB 22.114
Erdmassenberechnung nach REB 22.013
hierfür eine OpenOffice Tabellenkalkulation zum prüfen neu
Erdmassenberechnung mit Prismen nach GAEB-VB 22.114
mit einer animierten Darstellung!
DXF-Dateien
Lehrsatz des Pythagoras
Aufmaßregeln
Datenaustausch von Leistungsverzeichnissen
und wenn Sie noch Fragen habenGeländeaufnahme
-Verfahrensbeschreibung- Um ein Gelände in der nachfolgend beschriebenen Art mit Hilfe eines Computers auszuwerten ist es sinnvoll, das Gelände mit einem Tachymeter mit angeschlossenem Datenspeicher zu vermessen. Ein Tachymetermißt wie ein Theodolit Winkel und elektrooptisch Entfernungen. Diese Daten werden geräteintern in Koordinaten umgerechnet und gespeichert. Man kann sie an ein übergeordnetes Koordinatensystem anschließen, wenn von diesem System mindestens zwei Punkte in Baustellennähe bekannt sind. Andernfalls legt man für die jeweilige Baustelle ein örtliches Koordinatensystem fest. Es müssen dann aber mindestens zwei Bezugspunkte während der Arbeiten erhalten bleiben.
Das Tachymeter kann beliebig aufgestellt werden. Mann mißt die beiden Bezugspunkte an und kann dann alle für die Geländeaufnahme wichtigen Punkte vermessen. Die so gewonnenen Koordinaten werden zu einem Computer überspielt und können dann mit einem CAD-System zu Plänen verarbeitet werden. Auf dieser Grundlage werden dann alle weiteren Strecken, Flächen und Volumenberechnungen wie nachfolgend beschrieben erstellt.
Bei dem Vermessen erhält jeder Punkt eine Nummer, durch den dieser Punkt immer identifiziert werden kann.Streckenberechnung in der Projektion
-Verfahrensbeschreibung- In einem Koordinatensystem kann jede Strecke zwischen zwei Punkten mit dem Satz des Pythagoras berechnet werden. Die Wurzel aus der Summe der Differenz der X-Koordinaten zum Quadrat und der Differenz der Y-Koordinaten zum Quadrat ergeben die Entfernung.
Pythagoreischer Lehrsatz: a ² + b ² = c ²
Punkt 1001 X = 103,000 Y = 50,000
Punkt 1002 X = 100,000 Y = 54,000
Differenzen: 3,000 4,000
Für die Strecke zwischen Punkt 1001 und 1002 gilt:
Wurzel aus(3,000 ² + 4,000 ²) = 5,000 mDurch diesen Ansatz kann jede Entfernung in einem Koordinatensystem mit einem Taschenrechner ermittelt werden.
Streckenberechnung in der Abwicklung
-Verfahrensbeschreibung- Wie man eine Strecke in der Projektion berechnen kann, so kann man auch eine Strecke in der Schrägen berechnen: Man berechnet zunächst die Strecke in der Projektion. Dann zieht man die Wurzel aus der Summe der Strecke zum Quadrat und der Höhendifferenz zum Quadrat. Dies ist die Strecke in der Abwicklung.
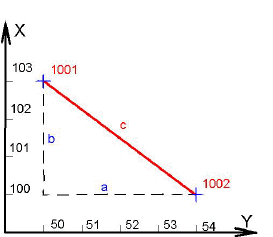
Pythagoreischer Lehrsatz: a ² + b ² = c ²
Punkt 1001 X = 103,000 Y = 100,000 Z = 10,000
Punkt 1002 X = 100,000 Y = 104,000 Z = 12,000
Differenzen: 3,000 4,000 2,000
Für die Strecke zwischen Punkt 1001 und 1002 gilt:
Wurzel aus(3,000 ² + 4,000 ²) = 5,000
Wurzel aus(5,000 ² + 2,000 ²) = 5,385 m
Durch diesen Ansatz kann jede Entfernung in der Abwicklung in einem Koordinatensystem mit einem Taschenrechner ermittelt werden.Flächenberechnung in der Projektion
-Verfahrensbeschreibung- Für die Flächenberechnung in der Projektion wird die Flächenformel nach Gauss-Elling angewandt. Dabei ist jede Fläche, deren Punkte im Uhrzeigersinn abgearbeitet werden, positiv. Wenn die Reihenfolge der Punkte entgegen dem Uhrzeigersinn eingegeben werden, so wird diese Fläche abgezogen.
Punkt X Y
1001 103,00 50,00
1002 100,00 54,00
1003 100,00 50,00
1001 103,00 50,00Gauss-Elling Formel: 2 F = Summe((Xi * Yi+1) - (Yi * Xi+1))
( 103,00 * 54,00 - 50,00 * 100.00 +
100,00 * 50,00 - 54,00 * 100,00 +
100,00 * 50,00 - 50,00 * 103,00 ) / 2 = 6,00 qmWenn Sie Elling zu Fuß rechnen wollen: hier ein lustiger Bastelbogen mit dem das Rechnen ganz einfach geht!
Und eine Möglichkeit mit einer Excel - Tabelle Flächen aus Koordinaten zu Rechnen!Flächenberechnung in der Abwicklung
-Verfahrensbeschreibung- Die Grundlage für die Flächenberechnung in der Abwicklung ist eine Dreiecksvermaschung. Für jede Dreieckseite wird die Länge in der Schrägen ermittelt (siehe Streckenberechnung in der Abwicklung). Dann wird die Fläche in der Schrägen mit der Heronschen Formel ermittelt.
Punkt X Y Z
1001 103,00 50,00 10,00
1002 100,00 54,00 10,50
1003 100,00 50,00 12,00Streckenberechnung in der Schrägen:
a Wurzel aus(4,00 ² + 1,50 ²) = 4,272
b Wurzel aus(3,00 ² + 2,00 ²) = 3,606
c Wurzel aus(5,00 ² + 0,50 ²) = 5,025Heronsche Formel: Wurzel aus [s (s-a) (s-b) (s-c)]
wobei s = (a + b +c) / 2
s = ( 4,272 + 3,606 + 5,025 ) / 2 = 6,4515
F = Wurzel aus [ 6,4515 ( 6,4515 - 4,272 ) ( 6,4515 - 3,606 ) ( 6,4515 - 5,025)]
F = 7,555 qmwie man mit einer Excel-Tabelle die Heronscher Formel rechnet
Dreiecksvermaschung nach GAEB-VB 20.404
-Verfahrensbeschreibung- Nach den GAEB - Richtlinien soll die Vermaschung als Delauney-Triangulation erfolgen. Zur Erklärung wird auf Literatur verwiesen. Diese besteht aber nur aus einer Beschreibung verschiedener Lösungsansätze ohne das eine Formel genannt würde. Es ist dort nur die Rede von „schönen Dreiecken“ ohne mathematisch zu definieren was ein schönes Dreieck ist. Es wird nur gesagt das ein spitzwinkliges Dreieck nicht schön sei.
Eine interessante Beschreibung der Delauney-Triangulation fand ich bei: http://www.geoinformatik.uni-rostock.de/einzel.asp?ID=477Aber wie ist dies mathematisch umzusetzen?
Laut GAEB können verschiedene Algorithmen benutzt werden da alle zu identischen Ergebnissen führen würden.
Dies kann ich mir nicht vorstellen.
Ich kann nur beschreiben, wie das von mir entwickelte Programm vorgeht:
· Es muß im CAD der äußere Rand (Linien im Uhrzeigersinn) festgelegt werden.
· Es können Aussparungen festgelegt werden (Linien entgegen dem Uhrzeigersinn).
· Es können Zwangskanten definiert werden: d.h. Böschungsunterkanten, Böschungsoberkanten und ähnliche topographische Linien.
Ausgehend von einer Grundlinie (Anfangs der Randlinie, später einer schon gebildeten Dreiecksseite) wird derjenige Punkt gesucht bei dem sich der größt mögliche Gegenwinkel zur Grundlinie ergibt (unter Berücksichtigung der Zwangskanten). Mit diesem wird dann das Dreieck gebildet.
Wenn Sie mit diesem Vorgehen nicht einverstanden sind oder eine bessere Lösung wissen können Sie mir gerne mailen .Erdmassenberechnung nach REB 22.013
Grundlage für die Erdmassenberechnung sind Dreiecksvermaschungen für ein "altes" und ein "neues" Gelände sowie die dreidimensionalen Koordinaten für die Eckpunkte der Dreiecksvermaschung. Für jedes Dreieck wird die Fläche nach Gauss-Elling berechnet und das Volumen (Fläche mal mittlere Höhe) bis zu einem Bezugshorizont ermittelt. Aus der Differenz der Volumen des "neuen" und des "alten" Geländes bis zum Bezugshorizont ergibt sich der Abtrag bzw. Auftrag. 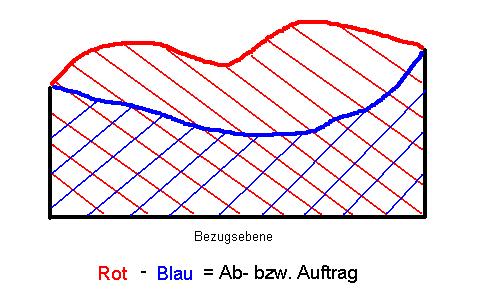
-Verfahrensbeschreibung-
Diese Methode kann nur angewandt werden, wenn die aufgenommenen Flächen des "alten" und des "neuen" Geländes deckungsgleich sind und keine Verschneidungslinie vorkommt, d.h. entweder nur Abtrag oder nur Auftrag.
Für den Datenaustausch enthält die REB-Verfahrensbeschreibung 22.013.pdf genaue Angaben wie Punkte und Dreiecke ab zu speichern sind. Um sich diese Daten anschauen zu können habe ich für die Tabellenkalkulation von LibeOffice Makros geschrieben welche die Daten in die Tabellen einlesen und berechnen. Diese LiebrOffice-Tabelle xyzVolumen.ods mit Beispiel-Dateien finden Sie in einer
.
In einer
finden Sie eine Anleitung für die xyzVolumen.ods Tabelenkalkulation.
Für Kritik, wenn etwas nicht funktioniert, oder wenn Sie Verbesserungsvorschläge haben, könen Sie mir gerne mailen.Erdmassenberechnung mit Prismen nach GAEB -VB 22.114
-Verfahrensbeschreibung- Grundlage für die Erdmassenberechnung sind Dreiecksvermaschungen für ein "altes" und ein "neues" Gelände sowie die dreidimensionalen Koordinaten für die Eckpunkte der Dreiecksvermaschung. Für jedes Gelände kann eine Höhendifferenz angegeben werden.Jedes Dreieck vom "neuen" Gelände wird in so viele Teilflächen zerlegt, wie Dreiecke vom "alten" Gelände deckungsgleich sind. Jedes dieser Polygone wird zunächst darauf geprüft, ob die Gelände sich verschneiden. Nach dieser Prüfung werden Auf- und Abtrag getrennt berechnet. Für jedes Polygon werden die Höhen für beide Gelände im Flächenschwerpunkt ermittelt. Aus der Differenz der Höhen, multipliziert mit der Fläche des Teil-Polygons, ergibt sich das Volumen. Bei Auftrag ist das Volumen positiv, bei Abtrag negativ.
Im Berechnungsprotokoll wird für jedes Dreieck das Volumen ausgedruckt, welches sich aus einer Vielzahl von Teilvolumina zusammensetzt. Um eine Vorstellung von dem Volumen zu ermöglichen, wird für jedes Dreieck die Fläche ausgedruckt, sowie eine Schicht-Stärke des Auf- bzw Abtrags, die sich aus Volumen dividiert durch die Fläche ergibt.
(Da das Programm zunächst das Volumen mit allen dem Computer zur Verfügung stehenden Nachkommastellen berechnet, ist es nicht sinnvoll Fläche mal Schichtstärke nachzurechnen, weil aus Gründen der Übersichtlichkeit nur drei Nachkommastellen ausgedruckt sind.)In der Spalte 'Lage' steht ein "T", wenn nur eine Teilfläche dieses Dreiecks von der Dreiecksvermaschung des "alten" Geländes abgedeckt wird. Ein "A" bedeutet, daß das Dreieck außerhalb der Dreiecksvermaschung des "alten" Geländes liegt.
animierte Darstellung
wußten Sie wie eine DXF-Datei aufgebaut ist? Die Endung DXF steht für "Drawing Interchange Format". Eine im ASCII-Code geschriebene DXF-Datei kann mit jedem Textverarbeitungsprogramm gelesen (und auch manipuliert) werden. Eine DXF-Datei beginnt mit dem „Header“, in dem Grundeinstellungen, Blöcke usw. festgelegt werden. Es folgt der Abschnitt „Entities“, in dem die eigentliche Zeichnung gespeichert wird. Es gehören immer zwei Zeilen zusammen: in der ersten Zeile steht eine Schlüsselnummer die angibt welche Information folgt. In der zweiten Zeile folgt die eigentliche Information. Hier ein Beispiel: DXF-Dateien
DXF-Datei 0
SECTION
2
ENTITIES
0
POINT
5
20
8
BEISPIEL
10
58.201
20
47.336
30
0.0
0
LINE
5
21
8
BEISPIEL
10
61.45
20
34.893
30
0.0
11
71.195
21
56.533
31
0.0
0
CIRCLE
5
22
8
BEISPIEL
10
77.692
20
44.631
30
0.0
40
5.831
0
ENDSEC
0
EOFDie Referenznummer benutze ich um die Punktnummer an den Punkt zu binden (dadurch ist kein Block notwendig).
Diese Angaben beziehen sich auf AutoCAD Release 12. Das DXF - Format wird (leider) ständig von Autodesk (den Erfindern dieses Formtes) weiter entwickelt. Ausführliche Information in Buchform finden Sie bei CR/LFder Nachweis vom Lehrsatz des Pythagoras
Nur zur Erinnerung, weil ich es immer wieder vergesse: Aufmaßregeln
Lt. DIN 18 320 „Landschaftsbauarbeiten“:
5.1.7 Boden wird getrennt nach Bodengruppen und, soweit 50 m Förderweg überschritten werden, auch nach Länge der Förderwege abgerechnet.
5.1.8 Bei Abrechnung nach Flächenmaß (m²), ausgenommen Flächen nach Abschnitt 5.1.9, werden Bäume, Baumscheiben, Stützen, Einläufe, Felsnasen, Schrittplatten und andere Aussparungen bis 2 m² Einzelgröße nicht abgezogen.
5.1.9 Bei den Naß- und Trockensaaten nach DIN 18918 werden Aussparungen und Durchbindungen wie Felsflächen, Bauwerke u. ä. bis zu 100 m² Einzelfläche nicht abgezogen.
5.1.10 Bei Abrechnung nach Längenmaß (m) werden Unterbrechungen durch Aussparungen und durchbindende Bauteile bis zu 1 m Länge nicht abgezogen.Seitenanfang
Wenn Sie wissen wollen was hinter den DatenArten 81 bis 86 steckt finden Sie hier einige Angaben. Datenaustausch von Leistungsverzeichnissen
und wenn Sie noch Fragen haben:
Georg Römer
Ing.(FH) Landespflege
Perhamerstr. 6
80687 München
Tel. 089 546 38 332
Fax 089 546 38 336post@xyz-roemer.de
(wird nur unregelmäßig abgeholt, wenn dringend bitte Anrufen)